Lab 5. Population Genetics

Notes:

Pre-lab Exercise can be found HERE
Bring a calculator to lab.
Link to PDF version of this handout.

Objectives:

Appreciate the importance of choice of genetic information to answer a particular evolutionary ques-tion.
Calculate and understand metrics to compare genetic diversity within and among populations for multilocus data.
Use genetic and ecological information to make an informed decision about conservation.

KEY WORDS: agarose gel electrophoresis; microsatellite; polyacrylamide gel electrophoresis; lo-cus/loci; polymorphic; monomorphic; observed heterozygosity; expected heterozygosity

1 Overview of Evolution

In Lab 4 (and upcoming in lecture), we’ve encountered the Hardy-Weinberg (HW) Model, a null hypothesis predicting that when no evolutionary forces are acting on a population, allele and genotype frequencies will be constant across generations. That is, a population in which allele and genotype frequencies are not changing is said to be in Hardy-Weinberg Equilbrium. The HW Model further predicts that within a single generation, the population’s allele and genotype frequencies will be in Hardy-Weinberg Proportions—that is, the proportion of each genotype present in the population is a direct function of the frequency of each allele in the same population (i.e., the frequency of A⁺A⁺ is simply the frequency of the A⁺ allele squared). Of course, if any evolutionary forces are acting then these relationships will not hold.

In nature the assumptions of the HW model are often violated and allele and/or genotype frequencies do change across generations (and may not be a direct function of each other). Because we have an understanding of the effects of each evolutionary force, we can make predictions about how allele and/or genotype frequencies will change when evolutionary forces are acting. In many cases, we can even predict the long-term (equilibrium) outcome, if the force continues to act in the same way for many generations.(Remember that equilibrium means a stable or unchanging state.)

One way evolutionary biologists describe changes in a population’s genetic structure is to think about (1) how the number of alleles is affected, and (2) how the frequency of heterozygosity is affected (i.e., are there more individuals that are heterozygotes or fewer?). The number of alleles and percent heterozygosity are both estimates of the amount of genetic variation in a population. Below, we consider the effects of each evolutionary force on the genetic variation in a population. In Lab 5, you will put this information into practice when you use information about the genetic variation present in several populations to make a decision about conservation.

Mutation

We’ll start with mutation, which is pretty easy to reason through even though it’s actually hard to detect new mutations in natural populations. Mutations are the original source of all genetic variation and include everything from a whole extra copy of a chromosome to the change of a single base from one nucleotide to another! Spontaneous mutations in the DNA sequence of an organism’s cells can happen at any time and may either be detected and repaired or, if not repaired, they may be passed on to daughter cells. In terms of evolution, only mutations that happen in cells that give rise to offspring are inherited across generations. Mutations can be beneficial (improve an organism’s survival and reproduction, or fitness), neutral (have no effect on fitness), or deleterious (reduce fitness). Most mutations will be neutral, occurring in sequences that are not part of a gene or regulatory region, since that’s most of the genome (only about 2% of the 3.2 billion base pairs in the human genome codes for proteins or functional RNAs)! Mutations are relatively rare, with only about 1 gene in a million being mutated per cell division. Even many mutations that do occur in a coding sequence will not have any effect on the an organism’s phenotype or fitness (remember the wobble position in codons?).

So, how does mutation affect genetic variation in terms of numbers of alleles and frequency of heterozy-gosity? New mutations create new alleles for a locus, increasing the number of alleles and heterozygosity, but just a tiny bit. The very first time the mutation occurs it will only be present in 1 individual and likely as a heterozygote. In most cases, where population sizes are large, that means the new mutation will not have much influence on allele or genotype frequencies in a population – it will only affect one locus at time and only introduce one new allele at that locus.

Genetic drift

Genetic drift is change in allele frequencies simply due to chance in who survives and reproduces – unrelated to the organism’s genotype. Because all populations have a finite number of individuals in them, drift occurs in every population of every living species. Mutations that arise and are neutral will change in frequency due to drift—that first new mutation could by chance not end up in any of the offspring produced by the organism and thus be lost from the population. Alternatively, a new mutation could, by chance, end up in half or more of the organism’s offspring and increase in frequency in the population. While all populations experience drift, chance has a bigger influence on allele frequency change in smaller populations than it does in large ones. For example, consider a locus with 2 alleles at equal frequency to each other (p = q = 0.5) in a population of constant size. If the population contains 10 individuals, then just by chance, 95% of the time we’d expect the allele frequency in the next generation to be anywhere from p = 0.27 to p = 0.73! However, if the population contained 100 individuals, then 95% of the time we’d expect the next generation’s allele frequency to be between p = 0.43 and p = 0.57, just by chance. The larger the population size, the less variation in allele frequency we expect to observe by chance.

Since genetic drift is stochastic, that means that in any given instance we can’t predict what’s going to happen—we can’t predict whether the frequency of an allele will increase or decrease. However, in the long-term, genetic drift eventually causes allele frequencies to “drift” away from their starting point until they, by chance, reach p = 0 (this is extinction of the allele from the population) or p = 1 (all individuals in the population are homozygous for the allele, which is fixation). The number of generations to extinction or fixation of an allele also depends on population size—a small population loses alleles and heterozygosity a lot faster than would a large population. Each locus in the genome will experience drift separately so some loci in the population’s genome will become fixed for a single allele while other loci will still have multiple alleles segregating. Because genetic drift is stochastic and happens independently in different populations, this also means that genetic drift will tend to cause different populations to diverge from one another, for example having different alleles for a given locus.

Gene flow

Gene flow is the movement of alleles from one population into another. This can happen by the movement or dispersal of adults from one place to another but can also result from the movement of just gametes. For example, pollinators can carry pollen from one plant population to pollinate flowers in another population, thus causing gene flow to occur. When an organism (or gamete) moves into a new population, they take all their genes with them so gene flow can change allele frequencies for all genes in the genome at the same time. Like genetic drift, the amount by which allele frequencies change depends how many individuals (or gametes) are moving in comparison to the population size, that is, the rate of gene flow. In a population of 10 individuals, 1 new individual per generation represents a rate of gene flow of 10% but in a population of 100 individuals, 1 new individual per generation represents gene flow of 1%. The higher the rate of gene flow, the greater the change in allele frequencies.

So how does gene flow influence genetic variation in terms of number of alleles and percent heterozygosity? On average, we expect gene flow to increase the number of alleles in a single population and thus also to increase heterozygosity. This is because we can think of gene flow as opposing genetic drift. Drift tends to reduce genetic variation while gene flow represents an increase of genetic variation, preventing alleles from going extinct. Of course, there are situations when gene flow reduces genetic variation (just like there are situations when drift increases genetic variation) but we usually want to consider the average expectation. Another thing to keep in mind with gene flow is that because it represents a genetic connection between different populations, gene flow tends to cause different populations to become more similar to each other.

Selection

Selection is change in allele or genotype frequencies of a locus due to differences between genotypes in their survival and reproduction (that is, their fitness). Selection will only occur for loci that encode information that can alter the phenotype–there are many non-coding regions of the genome in which different genotypes at those loci have no effect whatsoever on the organism’s survival or reproduction. When genotypes do differ in their ability to survive and reproduce, then we expect the genotype with the best survival and reproduction to increase in frequency in the population over time. Thus, we also expect the frequency of the allele(s) that make up that most fit genotype to increase over time. If the most fit genotype is a homozygote, then selection will reduce variation over time, eventually resulting in fixation of a single genotype (and thus fixation of a single allele) at a locus, given enough time. However, this reduction in number of alleles and heterozygosity due to selection will only affect the locus for which genotypes differ in fitness. Other loci in the genome will not lose variation due to selection on the first locus. For example, if there was selection favoring less hair in dogs, that would not lead to less coat color variation because hair density and coat color are caused by variation in different loci. While selection sometimes reduces genetic variation (when a homozygote has the highest fitness), in other cases it will increase or maintain genetic variation. For example, if the genotype with the highest fitness is a heterozygote, then selection will maintain genetic variation for that locus. Notice that what matters about fitness is not exactly how likely you are to survive or the exact number of offspring that you have, rather, what matters is a genotype’s survival and reproduction relative to that of other genotypes in the population.

A few other points to remember about selection: (1) selection acts on phenotype, not directly on the genotype, so it’s important to know what phenotype is affected; (2) for selection to act, there must be variation in the phenotype that is due to variation in the genotype—if there is no phenotypic variation then there cannot be selection happening; (3) when we think about selection, we should be thinking about the cause of the selection as well as the phenotypic trait that we think is experiencing selection. That is, if we think that a population of dogs living in the tropics is experiencing selection for less hair, then we also need to think about why having less hair would be beneficial to the survival and reproduction of the dogs in that population! For example, we might hypothesize that because the dog population is living in a tropical area, dogs with less hair thermoregulate better and thus have more energy to devote to making babies.

Nonrandom mating

Non-random mating is described as a mating pattern that deviates from that expected by chance alone. Which is to say, in a population that is “randomly mating” any individual is equally likely to mate with any other individual—or rather more precisely, that any female gamete has the same chance of mating with any male gamete in the gene pool. Some marine animals reproduce by a method that is very close to random mating—broadcast spawning. In mussels, for example, all of the males and females in the population release planktonic eggs and sperm that drift in the water column until they meet a gamete of the opposite type, at which syngamy occurs and development of the larva begins. In this scenario, mating is indistinguishable from random.

But, as you are probably aware, mating is non-random for many species. One type of non-random mating that is particularly common is inbreeding—mating with close relatives more often than expected by chance alone. The most extreme version of inbreeding is mating with yourself, or selfing, which may be possible in hermaphroditic organisms. Hermaphrodites occur in both plants (common in the Angiosperms, flowering plants) and animals (for example, a number of species of invertebrates such as Caenorhabditis elegans, snails, and barnacles). Interestingly, while some hermaphrodites are capable of self-fertilization, others are unable to fertilize their own gametes (or self-incompatible)! So we are led to wonder, how are allele and genotype frequencies affected by inbreeding? We’ll explore the answer to this question in the next section.

2 Studying Genetic Variation

Electrophoresis is a technique used to separate molecules in a gel or other medium according to size, shape, and charge. Today we’ll use data collected via electrophoresis of DNA fragments to study genetic variation. Gel electrophoresis allows us to collect genotype data for microsatellite loci in order to survey genetic variation among several populations. Next week in the Molecular Phylogenetics lab, we’ll examine genetic variation between the plant species we examined in Lab 2, by comparing the sequence of the rbcL gene. Both of these exercises study genetic variation, but they use different approaches and have different goals. For example, the sequence of the rbcL gene (which we are examining to construct an Angiosperm phylogenetic tree) varies between species, but there is almost no variation among individuals within a species. That is, each species essentially has only one allele for the rbcL gene. In contrast, if we want to study genetic differences among individuals within a single species and among multiple populations of that species, we must use loci that will be different in different individuals. An example of such loci can be found in microsatellites, which are short repetitive sequences of DNA (e.g., “CAAA” repeated 20 times) that experience a high rate of mutation. They are not usually involved in coding for any protein product so we consider them to be “neutral” loci; that is, the allele that is present does not affect survival and reproduction of the organism. Because these pieces of DNA mutate rapidly, there are many alleles within a species but the same locus often cannot be identified in distantly related species since they have accumulated too many random mutations independently. Thus, rapidly evolving loci like microsatellites help us to understand relationships within and among populations (for example, they are sometimes used to assign paternity or in forensics). Meanwhile, conserved coding regions (like rbcL) help us to understand relationships among diverse species, because the gene sequence is super similar within a single species but somewhat different in distantly related species (yet not so different that we can’t tell it is the same gene).

2A Microsatellite loci display genetic variation within species

Recall that a microsatellite locus is a repetitive piece of DNA, where a 2-6 base pair long unit is repeated many times. For example,

“ACACACACACACACACACACACACACACACACACACACACACAC”

In the above sequence, the unit is “AC” and it is repeated 22 times resulting in a length of 44 base pairs. This type of repetitive DNA mutates rapidly, easily growing longer or shorter by one or more unit at a time. An individual that has lost a repeat due to mutation will have 21 repeats and a fragment length of 42 base pairs. Thus, we will be examining variation in the number of repeat units—alleles will be defined by the length of the fragment of DNA. This differs from the example with rbcL above, where each species will have a fragment of the same length but the sequence of letters will differ among species.

Electrophoresis is a great technique for us to use to genotype microsatellite loci, because it separates molecules according to size. We consider each band in a different vertical position on the gel to be a different allele (with a different size). If a diploid individual has two different alleles, then you will see two bands of different length on the gel (a heterozygote). This feature makes microsatellite loci useful for population genetic studies, since we can tell who is homozygous (only a single band on the gel) and who is heterozygous (two bands on the gel).

Note: Microsatellites are just one example of the type of genetic locus used in population genetic studies. As the cost of sequencing decreases, sequence-based loci can be developed in which thousands to millions of loci are genotyped (usually using single-nucleotide polymorphisms, SNPs). Such loci are still considered neutral, like microsatellites. This is being referred to as population genomics instead of population genetics because the large number of loci means that loci are spread out, covering much more of the genome than would be true if one used 20 microsatellite loci.

2B Interpreting bands on a gel

So how do we genotype individuals from band position on a gel? Figure 1 shows a single microsatellite locus genotyped in 28 individuals of a rice-infecting fungus from a population in Brazil. Each column is called a “lane” and is the amplified DNA from a single individual; the first and last lanes are sizing standards. You can see that everyone in this population has the same allele and they are all homozygous for the allele—making this population monomorphic for this locus. In contrast, Figure 2 shows a different locus, for 24 individuals in a Brazilian population that is polymorphic for the locus—there are multiple alleles in the population.

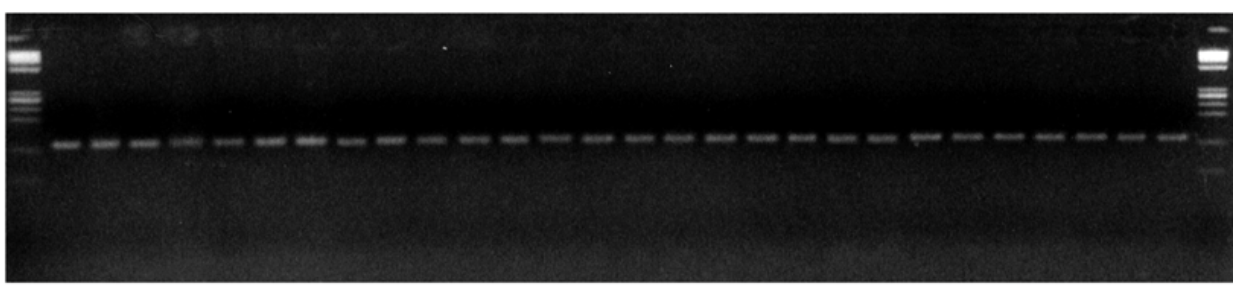
Figure 1: Banding pattern for a microsatellite locus (locus A) in a Brazilian popu-lation of a rice-infecting fungus. Brondani et al. (2000).

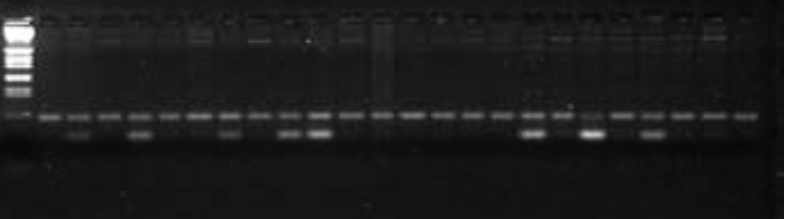
Figure 2: Banding pattern for a polymorphic microsatellite locus (locus B). Bron-dani et al. (2000).

When we genotype microsatellite loci we usually give the locus a unique name (here we will use locus A and locus B for the loci depicted in Figures 1 and 2, respectively). Then, we name the alleles with subscripts giving their fragment length (e.g., allele A₂₀₄ for a fragment of 204 base pairs in length). So a homozygote is A₂₀₄A₂₀₄ and a heterozygote might be A₂₀₄A₁₉₈.

Let’s calculate genotype and allele frequencies of locus B for the population in Figure 2 (you should be able to do the calculations for locus A as well). First, note that there are 2 alleles. We will call them B₁ and B₂, numbered starting at the top of the gel. Now we count how many individuals there are of each genotype:

\[B_1 B_2 = 16~~~~~~~~~~B_1 B_2 = 7~~~~~~~~~~B_2 B_2 = 1\]

And the observed frequencies of each genotype:

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $P_{obs} =$ frequency of $B_1 B_1 = \frac{16}{24} = 0.67$

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $H_{obs} =$ frequency of $B_1 B_2 = \frac{7}{24} = 0.29$

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $Q_{obs} =$ frequency of $B_2 B_2 = \frac{1}{24} = 0.04$

(Don’t forget to make sure the frequencies sum to 1.0!)

Next, calculate the allele frequencies in the population, either by counting them up or using the genotype frequencies:

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $p =$ frequency of the $B_1$ allele $= P_{obs} + \frac{H_{obs}}{2} = 0.67 + 0.145 = 0.815$

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $q =$ frequency of the $B_2$ allele $= Q_{obs} + \frac{H_{obs}}{2} = 0.04 + 0.145 = 0.185$

(Do the frequencies sum to 1.0? How would this calculation be different with more than 2 alleles?)

And the expected heterozygosity (from Hardy-Weinberg):

\[H_{exp} = 2pq = 2 \times 0.815 \times 0.185 = 0.302\]

Note that when measuring genetic variation among population we are usually most interested in the observed and expected heterozygosity.

2C Measures of genetic variation within populations

How can we summarize how much genetic variation is found within a population when we are studying multiple loci? There are several parameters that are commonly used to describe within population genetic variation, presented in Table 1. This table describes the genetic diversity present in loci A and B of the rice population, as depicted in Figures 1 and 2.

Variable	Description	Est
Table 1: Standard measures of genetic diversity used in population genetics.
Variable	Description genotype frequency	Estimated for Loci A and B
P	Percent of loci that are polymorphic	$\frac{1}{2}=0.5$
A	Average number of alleles	$\frac{(2+1)}{2}=1.5$
$\overline{\textit{H}}_{obs}$	Average observed heterozygosity	$\frac{(0.29 + 0)}{2}=0.145$
$\overline{\textit{H}}_{exp}$	Average expected heterozygosity	$\frac{(2×0.815×0.185)+(2×1×0)}{2}=0.150$

3 Collecting data about African elephant populations

The data in this lab derive from real elephant populations in Africa and they have been used to make recommendations about how many species of African elephants exist, which impacts how they are pro-tected (or not). As you work through the background info and genotyping loci, think about the following questions:

How many species should be recognized?
If not all populations can be protected, which ones should be chosen and how would you choose?
In considering future efforts, do you have any concerns about the processes that might be occurring in this system that could be detected in these genetic data?

3A Ecology of the African elephant

The African elephant, Loxodonta africana, once ranged from the Mediterranean Sea to the south coast of the African continent. But due to habitat destruction and fragmentation and poaching for ivory, today L. africana wild elephants are only found south of the Sahara in patchy habitat fragments (Figure 3). The population size of the species is thought to have been 3-5 million individuals in the 1930s, with current population size estimates between 75,000-300,000 wild African elephants. However, that number consists of many isolated populations of elephants, rather than a single intermixed group (unlike humans, elephants must rely on their own four feet alone to get anywhere). Individual populations may experience large declines in any given year, sometimes losing 80% of the population to poaching. Given the fragmentation of the habitat, decimated local populations may not have access to more distant populations or better habitat to recover from such events.

In addition to threats to their habitat and survival, it seems that not all elephants are ecologically the same. Two distinct types have been recognized within African elephants—forest populations and savannah populations. These groups exhibit differences in their food preferences, habitat, and morphology. On the basis of these differences, some scientists have suggested that forest elephants and savannah elephants be classified as different species or subspecies (forest: L. africana cyclotis; savannah: L. africana africana).

Designating two (or more) species rather than one would have important consequences for international conservation law and efforts. In particular, a larger fraction of the total population of African elephants would be protected if two or more sub-groups were recognized. However, some scientists have argued that these two varieties do not merit distinction as different species, given molecular data that supports a history of hybridization between forest elephants living on the edge of the forest habitat and adjacent savannah elephants.

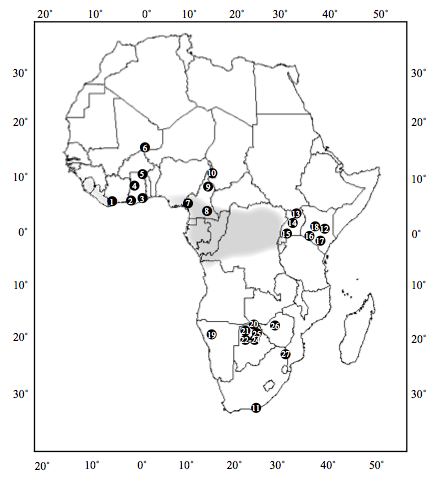
Figure 3: Geographic distribution of African elephant populations. Grey shaded areas indicate current forest zone. Site numbers correspond to populations in the table below. From Eggert et al. (2002)..

Site	ID	Population Name	Habitat
1	Tai	Tai National Park	forest
2	Bia	Bia National Park	forest
3	Kakum	Kakum National Park	forest
4	Mole	Mole National Park	savannah
5	RVV	Red Volta Valley	savannah
6	Mali	Mali Gourma	savannah/desert
7	Bmbo	Bmbo (Banyang Mbo Forest Reserve)	forest
8	Dja	Dja	forest
9	Benoue	Benoue	savannah

3B Genotyping loci

Each group will receive gel diagrams for 2 populations and 3 microsatellite loci, with 10 individuals sampled per population. In addition to your focal populations, you will have a copy of gel diagrams for all of the other populations so that you can make certain comparisons. In pairs, calculate the following parameters for each of the 3 loci for 1 population, calculate the averages, then proof the data for the other pair’s population. Use the formulas and procedures in the examples, and show your work on the last page of this handout. If you run out of room, you may add another sheet to display your work. After you calculate the measures of diversity for each locus in a population, remember to then calculate the average values across the three loci for each population.

Note: For each locus, “unique” alleles are only found in a single population. Use the additional sheets in the packet to determine whether you have any unique alleles. Remember, alleles are identified by vertical position of the band. A^∗ also refers the number of unique alleles. (column 5 in the tables below)

pop	loc	poly	no_allele	no_unique	hobs	hexp
Population ID	Locus	Polymorphic (0 = no, 1 = yes)	No. of alleles	No. of unique alleles	$\textit{H}_{obs}$	$\textit{H}_{exp}$
_	La1	_	_	_	_	_
__	La4	__	__	__	__	__
___	La17	___	___	___	___	___
Averages for the 3 loci		P	A	A*	$\overline{\textit{H}}_{obs}$	$\overline{\textit{H}}_{exp}$
Averages for the 3 loci		_		_	_	_

pop	loc	poly	no_allele	no_unique	hobs	hexp
Population ID	Locus	Polymorphic (0 = no, 1 = yes)	No. of alleles	No. of unique alleles	$\textit{H}_{obs}$	$\textit{H}_{exp}$
_	La1	_	_	_	_	_
__	La4	__	__	__	__	__
___	La17	___	___	___	___	___
Averages for the 3 loci		P	A	A*	$\overline{\textit{H}}_{obs}$	$\overline{\textit{H}}_{exp}$
Averages for the 3 loci		_		_	_	_

Record your data on the board with everyone’s data and copy into Table 2 below.

pop	p	A	A_star	Hobs	Hexp
Table 2: Table of population genetic data for 9 populations of African elephants.
Population	P	A	A*	$\overline{\textit{H}}_{obs}$	$\overline{\textit{H}}_{exp}$
Benoue	_	_	_	_	_
Bia	_	_	_	_	_
Bmbo	_	_	_	_	_
Dja	_	_	_	_	_
Kakum	_	_	_	_	_
Mali	_	_	_	_	_
Mole	_	_	_	_	_
RVV	_	_	_	_	_
Tai	_	_	_	_	_

Remember: A^∗ is the number of unique alleles in a population. These are alleles for a given locus that occur in only this poulation. It is important for you to consider the implications of unique alleles with respect to the evolution of these populations.

4 Pre-Lab Exercise

Read section 1 Overview of Evolution before proceeding to complete this exercise.

Practicing thinking about inbreeding and genetic variation

Let’s work through an example thinking about inbreeding in a self-compatible hermaphroditic plant and a locus that influences flower color. Homozygous wild type plants have red flowers (A⁺A⁺), heterozygotes have pink flowers (A⁺A^w), and homozygotes for the white allele have white flowers (A^wA^w). Let p = frequency of the A⁺ allele and q = frequency of the A^w allele. For the purposes of this exercise, we’ll assume that flower color has no effect on the ability of the plant to survive, nor on how many offspring it can produce (all flower colors have the same fitness).

The following questions will guide you through thinking about the effects of non-random mating (specifically in-breeding) on allele and genotype frequencies, both after one or a few generations and in the longer-term equilibrium situation.

Let’s start with a population that is in HW Equilibrium with p = 0.3 and q = 0.7. This is the parent generation (P). What are the genotype frequencies, as predicted by the HW Model?

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ A⁺A⁺ = p² = ___________ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ A⁺A^w = ___________ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ A^wA^w = ___________

Now, let’s allow each plant to reproduce only by selfing (pollinating its own flowers). What will be the proportions of offspring with each genotype produced by each type of mating? (Note: the answers are already provided for A⁺A⁺ × A⁺A⁺ parents.)

Genotype	AA	AAw	AwAw
Offspring genotype (F1)	Parental Genotype
Offspring genotype (F1)	A+A+	A+Aw	AwAw
A+A+	[a] 1.0	[d]	[g]
A+Aw	[b] 0.0	[e]	[h]
AwAw	[c] 0.0	[f]	[i]

Now, what are the total frequencies of each genotype in the population of all offspring? Note we need to weight the values in the table above by the frequency of each genotype in the population of parents. (This is similar to when we had to adjust for sex ratio in Lab 4.)

For example, for A⁺A⁺, the F₁ frequency of the genotype will be:

[a] $×$ (freq of A⁺A⁺ in parents) $+$ [d] $×$ (freq of A⁺A^w in parents) $+$ [g] $×$ (freq of A^wA^w in parents) $= 1.0 × 0.09~+~...$

Genotype

Phenotype

freq

Genotype

Phenotype

Offspring genotype (F1)

A+A+

red flowers

=

A+Aw

pink flowers

=

AwAw

white flowers

=

From these genotype frequencies, calculate the allele frequencies for this offspring population:

allele

homo

variable

freq

Allele

Homozygous phenotype

Variable

Frequency in the F1

A+

red flowers

p

=

Aw

white flowers

q

=

Genotype	Phenotype	freq
Genotype	Phenotype	Offspring genotype (F1)
A+A+	red flowers	=
A+Aw	pink flowers	=
AwAw	white flowers	=

allele	homo	variable	freq
Allele	Homozygous phenotype	Variable	Frequency in the F1
A+	red flowers	p	=
Aw	white flowers	q	=

Are the genotype frequencies in the F₁ different from those in the P generation (see Question 1)? If yes, describe the pattern.

Are the allele frequencies in the F₁ different from those in the P generation (see Question 1)? If yes, describe the pattern.

If selfing continues in this population for a long time, what do you think will be the allele and genotype frequencies after many generations? Briefly explain your reasoning.

From this example, we can see how selfing affects allele frequencies and genotype frequencies for a single locus. Do you think selfing only affects frequencies for this single locus in the plant’s genome?Briefly explain your reasoning.

Selfing is common in nature—but so is outcrossing! (Ah, diversity!) This suggests to us that neither selfing nor outcrossing is likely to be the best solution to all possible scenarios.
1. Can you think of conditions in which the organism might have higher reproductive success by selfing? (That is, selection favors selfing.)
2. What about a case where the organism reproduces more effectively by outcrossing? (That is, selection favors outcrossing.)

In real populations mating is unlikely to be the extremes of only random mating or only selfing. For example, in many plant species, an individual will produce some seeds through outcrossing but also a fraction of seeds through selfing (e.g., jewelweed, Impatiens capensis). This is known as a mixed mating strategy. In a few sentences, explain how you think a mixed strategy will affect allele and genotype frequencies. Compare to selfing and to outcrossing.

If we are examining a natural population and we estimate allele and genotype frequencies, we can then use that information to estimate f , which represents how much inbreeding is reducing heterozygosity in our population compared to a random mating population. To do this, we compare the observed frequency of heterozygosity to the expected frequency of heterozygosity (from HW proportions) using the following equation:

\[f = 1 - \frac{H_{obs}}{H_{exp}}\]
When $f = 0$, there is no inbreeding, the population is mating randomly and the observed heterozygosity equals the expected heterozygosity. When $f = 1$, the population is completely inbred and there is no observed heterozygosity.

Now, let’s use this in an example. Calculate $f$ for the population with the following observed genotypic frequencies. (Show your work.) Is this population experiencing inbreeding?

Genotype

Phenotype

Genotype

Observed frequency

A+A+

0.553

A+Aw

0.294

AwAw

0.153

Genotype	Phenotype
Genotype	Observed frequency
A+A+	0.553
A+Aw	0.294
AwAw	0.153

5 Post-Lab Assignment (due in Lab 6)

Once all data are collected, recorded on the board, and recorded in your lab handout, you are ready to begin the post-lab assignment! Work with your group to answer the questions below.

Refer to Table 2 of the genetic data for all 9 elephant populations in responding to the questions below. You may also wish to reference the map in Figure 3. The data table reports 5 measures of genetic variation.

Why do you think we use multiple measures and how do they differ from each other?

Why might observed and expected heterozygosities differ? What could cause that?

Of the 9 elephant populations for which you have data, which do you think is the most genetically variable? Explain why, referring to specific data from the table to support your argument. A few sentences are sufficient.

Of the 9 elephant populations for which you have data, which do you think is the least genetically diverse? Explain why, supporting your argument with specific data from the table. A few sentences are sufficient.

If you had funding to direct conservation efforts for two and only two of these 9 populations, which would you choose? Explain why, in one meaty paragraph. Be sure to make a scientific argument supported with data.

March 05 & 21, 2024