Lab 7. Adaptive Morphology of N. American Redbud Trees (*Cercis canadensis*) • biol200

1 R Tutorial: Pre-lab Exercise

This week we will collect some data on leaf shape using images of herbarium specimens (more explanation later). We will conduct several different statistical analyses and graph our data. To visualize the data and perform our analyses, we will use the statistical software package R via RStudio, accessed through a web browser. If you have taken STAT 113 or 114, you will be somewhat familiar with R and RStudio. However, in case you have not already encountered R, the pre-lab for this week will introduce you to the basics of using R for graphing and analysis of data. Pay attention and take notes as we’ll be using R for several upcoming labs!

Complete the tutorial below and turn in an electronic copyof the following at the start of your lab period this week:

A list of the R functions that you used to complete this exercise and brief descriptions (in your own words) of what each function does and how to to use it.

A scatterplot for the compensation dataset, created in R, with points differentiated by grazing treatment (using shape and/or color).

A paragraph describing the pattern that you see in the scatterplot—what was the hypothesis and pre-diction? Do the results you see in the graph support the hypothesis? Explain.

1A Getting Started with R

R is a free, open-source program for the analysis and visualization of data, created and maintained by statisticians. In the past 10 years, R has become the program of choice for statistical analyses in Biology and other sciences. R is different from other programs you might be used to—it requires you to write code in the R language in order to do the analysis (it’s not point-and-click or menu-driven). To make it easier for us, we’re going to use R through another program, the user-interface RStudio. The RStudio program is also free and provides us with some useful windows and menus.

We will be accessing RStudio through a web browser—RStudio is installed on a server at Oberlin. This means we don’t have to worry about installing on personal machines and you can easily access the program (and the files you upload) from any computer with internet access! Your login username is your Bb/email username (typically first initial, first 7 letters of last name, sometimes with a number added) , all in lowercase. Your password is your username plus 123 on the end (unless you have previously used the RStudio server and changed your password). For example, my dog Oberon’s username would be “oroles” and his password would be “oroles123”. You can login at: http://rstudio.oberlin.edu.

After you login, you need to change your password as it will expire and no longer work if you do not. You only need to do this if this is your first time using the RStudio server. Find and click on the Terminal tab then type “passwd” and enter to reset your password. You will be prompted to supply a new password. Make sure it’s something you can remember – it will not by synced with your email and Bb passwords! Note: when you type passwords into the terminal, it will not show which can be a little confusing. Trust that you are typing the password and be careful to type the correct password.

To use R, you will be writing commands and then executing them, with R providing the results of whatever you just told it to do. It is VERY IMPORTANT that you are extremely careful to write all of the commands EXACTLY as they appear—R will notice any differences in the position of periods, commas, parentheses, uppercase vs. lowercase letters. If you type something incorrectly, R will not be able to interpret it. If you get an error, the first thing you should do is make sure you typed the command in correctly!

A few things to keep in mind as you learn to use R:

You need to be aware of what operating system you are using (i.e., version of Windows or Mac OS) and that specific commands can sometimes depend on whether you are using a Windows machine or a Mac/Linux machine.
You need to know how to create folders and files on your computer—and know where they are stored (their file path). It’s important to make sure you know where you are storing your files and folders, the “PATH” to those files on your computer. On Windows, this typically involves a drive name, a colon (:), and slashes (e.g., “C:\MyDocuments\BiologyLab\data.csv”). On a Mac or Linux/Unix system, this includes the name of the drive, the name of your home directory, the names of folders, and slashes (e.g., “Users/username/Documents/BiologyLab/data.csv”).
You should be able to type your raw data into a spreadsheet or text file, such as Excel, Numbers, or Google Sheets. You should also be able to export that file as a comma-separated values (CSV) file type. This makes getting your data into R very straightforward.
WHATEVER YOU DO, DO NOT COPY AND PASTE TEXT FROM THIS HANDOUT. YOU NEED TO MANUALLY TYPE ALL OF THE COMMANDS. When you copy and paste into R, sometimes not all the characters copy correctly OR invisible characters get copied that cause problems for R. Plus, copying and pasting does not help you practice being careful, a crucial skill for any scientist!
You need to be able to type commands into your computer to be carried out by R. You MUST be very careful to type instructions exactly correctly—your computer cannot interpret an instruction that is missing a letter, for example, or when a letter is uppercase that should be lowercase. If you get an error message, the first thing to do is carefully proofread your work!
As you complete the tutorial, run one line of code at a time and make sure it seems to have worked correctly. If you run many lines of code at one time and get an error message, you will have trouble finding the error.

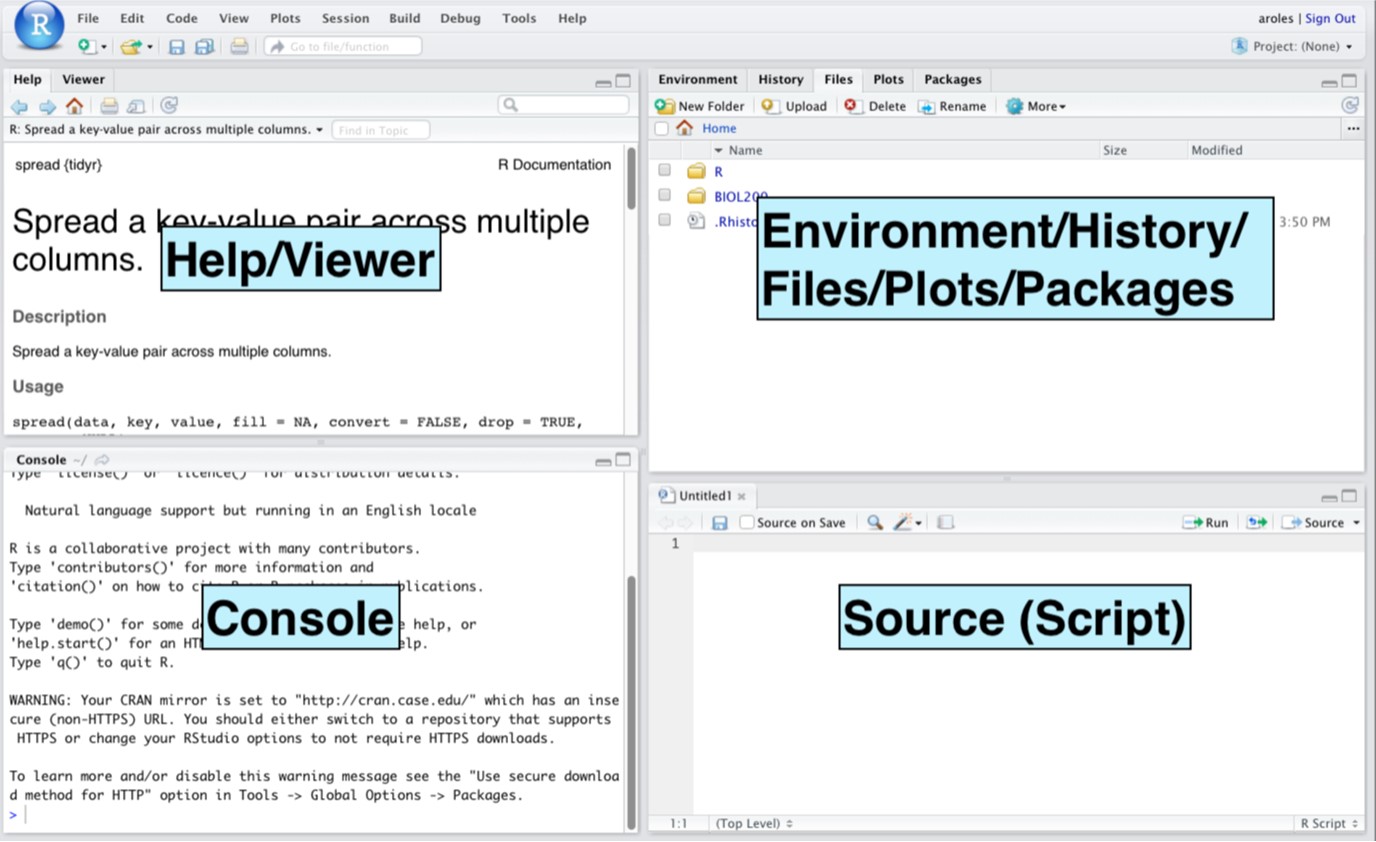
Figure 1: Screenshot of the RStudio window.

1B Orientation to R Studio layout

Open R Studio in your browser by going to http://rstudio.oberlin.edu. Once you’ve successfully logged in you should see a window like in Figure 1.

Here’s a brief description of the different parts of the RStudio window:

Console: This pane is where you enter code at the prompt (>), then press enter to run the code and the results or output show up. R is ready to take new lines of code when the prompt (>) is showing.
Source: This pane is where you can type commands into a script (a text file) that you can save to refer to later (e.g., if you want to re-run the analysis or remember how to do various things). Lines of code that are currently selected in the Source pane can be run (executed) in the Console by pressing Ctrl+Enter (PC) or Command+Enter (Mac).
Environment: In the Environment tab you can see any objects you have created in this R session (such as imported datasets under Data). Clicking on an item will cause a view window to open in the Source, letting you see the dataset in spreadsheet form (only for viewing, not editing).
History: The History tab shows you the lines of code that you have recently executed in the Console.
Files: The Files tab lets you navigate through files and folders in your directory (on the server, not on your computer).
Plots: Anytime you make a plot of your data, it will show up in the Plots tab. You can also view previous plots in this tab or export the current plot as an image or PDF file.
Packages: A list of the packages currently installed in R. Some packages are installed by default but there are lots of other packages available that encode additional functions not found by default. These can be installed by the user when needed. Packages that are currently loaded have a check in the first column.
Help: If you type a question mark before any function R knows, it will open up a Help page in this tab (for example, if you wanted info on the structure function, you would type ?str at the Console prompt).
Viewer: The Viewer tab allows you to see web content within R Studio.

1C Changing settings in R

Before we get started working in R, let’s make some changes to the default settings to make it easier to use.

Go to Tools $\rightarrow$ Global Options… In the box that pops up, click on Code and then make sure the box is checked for “Softwrap R source files”.

1D Importing and accessing the dataset

For this exercise, we’re going to go through the steps of importing a dataset, viewing it, and doing some graphing, just to get a feel for how R works. We’ll use a data file called “compensation.csv” as our example. You can download this file with the link below and save it to your computer.
The next thing we need to do is set up an R script—this will be like a notebook where we record everything we do and make notes for ourselves to help us remember later.

To start a new script in RStudio, go to File $\rightarrow$ New File $\rightarrow$ R Script. This script is where you will write your instructions for R before executing them and it will serve as a record of what you’ve done—useful later when you want to do similar things with a different dataset! We’ll also take notes about what we’re doing so we can use these commands later with different data sets.
TIP: In a Script file, any line that you start with a hash sign (#) will be ignored by R (not executed), so you can use this to leave notes and explanations for yourself.

Type the name of this exercise, your name, and today’s date into your script, using the # so R will not try to execute these notes:
```
# BIOL 200 pre-lab R tutorial
# yourname
# today’s date
```

To import the “compensation.csv” file into RStudio, in the Files pane, click Upload, navigate to the file location on your computer, and import the file into RStudio. Now RStudio can see the file but it has not made the data available to R itself. For that, we need to tell R to read the file and save it into memory with a name that we choose.

First, let’s load a package that contains lots of useful functions, the tidyverse package:
```
library(tidyverse)
```
Now, let’s just look at the file:
```
# read.csv tells R to read the file and print it to the screen 
#  but NOT to remember it
read.csv("compensation.csv")
```
To save the file to memory, we have to tell R what name we want it to use for this object:
```
# save the file to memory as the object called ‘comp’ 
#  but do NOT print the data to the screen
comp <- read.csv("compensation.csv") 
```
What you just did was tell R to read the compensation.csv file and save it as an object called comp. You can check to make sure it worked by asking R to list all of the objects that it knows right now. Type the following into the Console and press enter:
```
# Ask R to list the objects that it has saved in the workspace (R’s memory)
ls()
```
R will return a list with 1 object, your new object, “comp” which will look like this:
```
## [1] "comp"
```
If you type the following at the prompt, R will print out the dataset:
```
comp  # print out the object "comp"
```
Now, imagine that you want to use this dataset later. You type:
```
Comp
```
What happened? Why didn’t R print out the object for you?
That’s just an example of the kinds of error messages you might get if you make mistakes in your code.

Now that you have an object saved in memory, this means you can access information about the dataset, summarize it, manipulate it, or view particular parts of it using the name of the object. For example, you can get info on how many columns and rows are in the dataset and the attributes of those variables using the structure function, str(), like so:
```
str(comp)  
```
```
## 'data.frame':    40 obs. of  3 variables:
##  $ Root   : num  6.22 6.49 4.92 5.13 5.42 ...
##  $ Fruit  : num  59.8 61 14.7 19.3 34.2 ...
##  $ Grazing: chr  "Ungrazed" "Ungrazed" "Ungrazed" "Ungrazed" ...
```
Prints information about the object:
- its class (data.frame)
- number of observations (40 rows)
- number of variables (3 columns)
- names of columns
- type of data in each column (e.g., numeric, character – this is categorical)
You can see that the comp dataset has a column called “Fruit” (a continuous measure of the response variable fruit production), a column called “Root” (a continuous measure of the explanatory variable initial root diameter), and a column called “Grazing” (a character, or categorical, explanatory variable with 2 levels—Grazed and Ungrazed).

You can also view just part of the data set. The function head() returns the first 6 rows of data while the tail() function returns the final 6 rows of data.
```
head(comp)  # print the first 6 rows of the dataset
```
```
##    Root Fruit  Grazing
## 1 6.225 59.77 Ungrazed
## 2 6.487 60.98 Ungrazed
## 3 4.919 14.73 Ungrazed
## 4 5.130 19.28 Ungrazed
## 5 5.417 34.25 Ungrazed
## 6 5.359 35.53 Ungrazed
```
```
tail(comp)  # print the last 6 rows of the dataset
```
```
##     Root Fruit Grazing
## 35 9.351 98.47  Grazed
## 36 7.066 40.15  Grazed
## 37 8.158 52.26  Grazed
## 38 7.382 46.64  Grazed
## 39 8.515 71.01  Grazed
## 40 8.530 83.03  Grazed
```

1E Describing and summarizing the data

Ok, now that you have a dataset to work with, let’s see how to do some basic graphing and statistics. R has lots of built-in functions that help you to do the calculations you’re interested in—and to make beautiful graphs!

Remember that the comp dataset contains 3 columns: Root, Fruit, and Grazing. What do you think might be the hypothesis the researchers were studying? What do you think they predicted would happen in grazed versus ungrazed treatment groups? Why do you think they also measured initial root diameter? Once you’ve thought about those things a little bit, we can move on to checking out what fruit production (our response variable) looks like in this data.

Let’s start simple: you want to see what the variation in fruit production looks like and calculate some means. There are several ways to do this, the simplest using the function mean(). (Note: You can use the help function to find out more about any of the functions R knows, just type a question mark before the name of the function: ?mean. A window will open with a help page describing the function and its possible arguments.)

Now let’s use those functions with your dataset. Rather than just print the results to the screen, let’s save the result to an object so you can use it again later:

compSummary <- comp %>%
group_by(Grazing) %>%
summarize(samplesize = n(), # determine sample size 
          MeanRoot = mean(Root), # determine the mean of Root
          StdevRoot = sd(Root), # determine the standard deviation of Root
          MeanFruit = mean(Fruit), # determine the mean of Fruit
          StdevFruit = sd(Fruit)) # determine the standard deviation of Fruit

# The summary will is saved as the dataframe called 
#  "compSummary" with columns for the sample size, means, and 
#  standard deviations (sd) of Fruit and Root 
#  for each level of grazing

) Print the compSummary object to the screen. How does fruit production relate to grazing treatment? Do the plants in the Ungrazed group have the same initial Root diameter as those in the Grazed group?

1F Basic Graphing

Now you’re nearly ready to make a graph of the data. First, though, you should think about what pattern you might expect to see among these variables. This dataset describes the Fruit Production of a sample of plants. Some were grazed by insect herbivores (Grazed) and others were protected (Ungrazed). It also contains the Initial Root Diameter of all of the plants. How do you think fruit production would be affected by the presence/absence of grazers? What does initial root diameter have to do with anything?

You might think that initial root diameter (an explanatory variable) could influence potential fruit production (the response variable), regardless of whether plants were grazed or not. Let’s see what the relationship looks like for the ungrazed plants only, using a scatterplot (because you have two continuous variables to plot, Root and Fruit). First, you’ll subset the data, then you’ll plot it.

Does the pattern match what you expected? You could make this graph look nicer, giving it informative axis labels and a title. To do that, you need to add some code:
```
# Dotplot of fruit production versus grazing treatment
comp %>%
  filter(Grazing == "Ungrazed") %>%
  ggplot() +
  geom_point(mapping = aes(x = Grazing, y = Fruit, col = Grazing)) # Makes dotplot
```
```
# Boxplot of fruit production versus grazing treatment
comp %>%
  filter(Grazing == "Ungrazed") %>%
  ggplot() +
  geom_boxplot(mapping = aes(x = Grazing, y = Fruit, col=Grazing)) # Makes boxplot
```
Hey, what happened! It looks like there’s no data for the grazed plants! You must have made a mistake in your code. How can we make it show all the data, not just the ungrazed plants? Check the code carefully, correct the mistake, and then create the plot.
Our last step is to save a copy of this graph to turn in for the pre-lab assignment. This will require 2 steps, (1) save the plot to your home directory in RStudio, and (2) export the file from RStudio to the computer on which you are working.

This concludes the pre-lab exercise. Remember to hand in the assignment.

2 Background

Today in lab we will be using morphometric techniques to quantify spatial variation in leaf morphology across the geographic range of the eastern redbud (Cercis canadensis) in order to test the hypothesis that the variation is adaptive. The eastern redbud is common across much of the Eastern United States, with a range that extends south from northern Pennsylvania into northern Florida, and west into Texas (Figure 2). Though their leaves are generally cordate, or heart-shaped (Figure 3), the size and shape of the leaf varies across the species’ range. In areas further north and east, leaves tend to be larger, the apex (the pointed tip of the leaf; Figure 4A) tends to be more acute, and the sinus (the curve at the base of the leaf; Figure 4B) tends to be shallower. Conversely, in areas further south and west, leaves tend to be smaller, the apex tends to be less acute, and the sinus tends to be deeper.

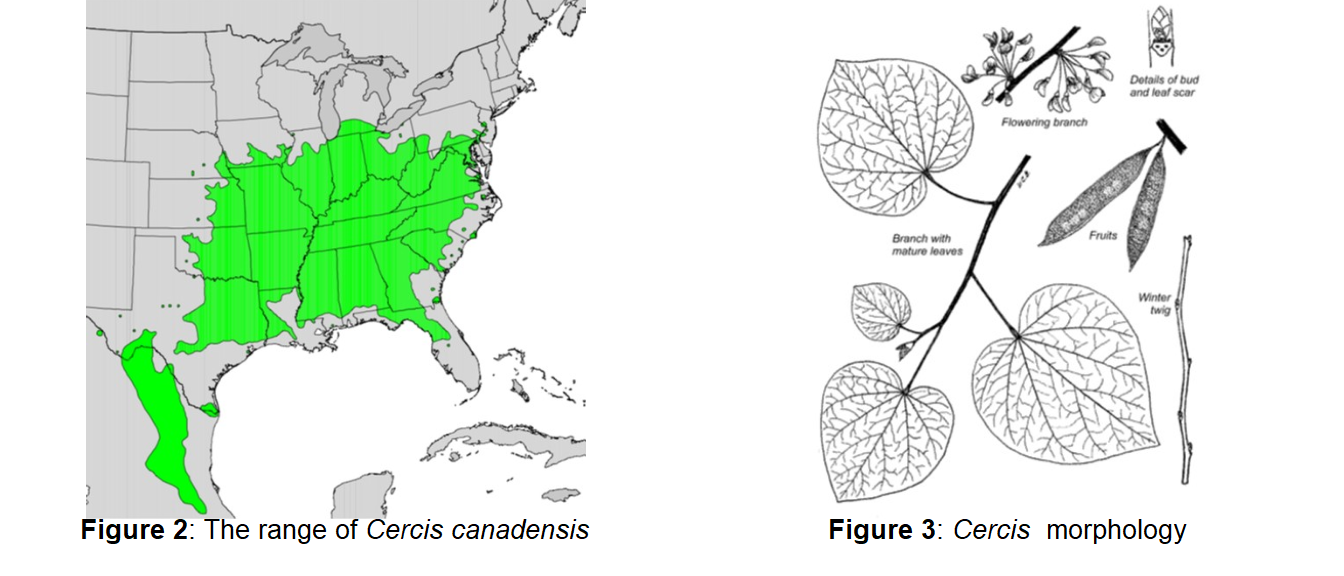
It’s hypothesized that this cline in size and shape is an adaptation to the climate an individual experiences. The climate further north and east in this region tends to be cooler and wetter, while the climate further south and west in this region tends to be warmer and drier. From the hypothesis, we might predict that the acute leaf tip serves as a drip tip to funnel water off the surface of the leaf in cooler, wetter climates, and that smaller leaves lacking an acute apex minimize surface area to reduce water loss in warmer, drier climates.

We will be testing morphological predictions of the hypothesis using morphometrics, the quantitative study of the form of an organism. In botany, morphometrics are most often performed on physical specimens of plants from an herbarium, a collection of preserved plant specimens. However, many herbaria (the plural of herbarium) have begun scanning their collections and making them freely available online for easy use by people outside their institution. Today, we will be performing morphometrics on digital images of plant specimens from the Freisner Herbarium at Butler University in Indianapolis. Because herbaria often specialize in the flora of their region, all of the specimens we’ll be measuring today were collected in Indiana. However, we will be pooling the data we collect today with a dataset from the California Academy of Sciences that spans the range of Cercis in Eastern North America.

You will be measuring the size of leaves (lengths and widths; Figure 5) for which we already have data about the apex and sinus shape, and the latitude, longitude, and elevation. The data set also contains climatic variables that represent the mean temperature and mean precipitation for the location from which each specimen was collected. These data were downloaded from WorldClim, an online database of global climatic data.

3 WorldClim Dataset

Before we start recording measurements, let’s look at and think about the WorldClim data. Find the file “Cercis.All.BioClim.csv” in the zip folder you downloaded earlier on your computer and then upload the file into RStudio http://rstudio.oberlin.edu. Remember you can check the pre-lab if you don’t remember how to upload the file.

Load the tidyverse library so we have the functions we need:

library(tidyverse)

Now use the read_csv() function to assign the file as an object in R (called “bioclim” below) and then use the names() function to see the names of the variables in the dataset:

bioclim <- read_csv("Cercis.All.Bioclim.csv")
names(bioclim)

##  [1] "...1"         "Record.No."   "Herbarium"    "Accession.No" "Collector"   
##  [6] "Colln.No."    "Mo"           "Day"          "Year"         "State"       
## [11] "County"       "Locality"     "Description"  "Latitude"     "Longitude"   
## [16] "Elevation"    "Mean.Temp"    "Mean.Precip"  "Apex.Shape"   "Sinus.Shape" 
## [21] "Lf.Length1"   "Lf.Width1"    "Lf.Length2"   "Lf.Width2"    "Lf.Length.Av"
## [26] "Lf.Width.Av"  "WL.Ratio"     "Lf.Area.Prox"

For each sample, the dataset contains information about the herbarium from which it came, its number in that herbarium, who collected it, when it was collected (some of these plants were collected before the Civil War and are still preserved in herbaria today), and a description of where it was collected, in addition to the latitude (°N), longitude (°W), elevation (meters), climatic information (mean temperature in °C and mean precipitation in mm), and leaf morphology measurements.

Use View(bioclim) to look at the object in the View window. Scroll further to the right in the datasheet and notice that the first 446 samples have all of their leaf size and shape info filled in already. The last 10 samples, however, are missing that information. In this week’s lab, you will be performing your measurements on those plants.

To prepare, you need to generate the hypothesis and predictions you have for this dataset, based on the information available to you. Subsequent to recording your leaf morphology measurements, you will carry out statistical analyses to test your predictions. Answer the following questions to describe your dataset, generate your hypothesis, and define testable predictions.

Consider the variables found in the bioclim dataset. Each column represents a variable that is either a response or explanatory variable. Which do you think are response variables? Explanatory variables? Each variable is also either quantitative (aka continuous) or categorical (aka discrete). Some variables, like apex shape, are coded numerically but are not continuous in the way “length” is continuous. However, order does matter—an apex shape of 4 is “bigger” (more pointed) than an apex shape of 1. This is called an “ordinal” variable. For this lab, you will treat such ordinal variables as quantitative rather than categorical variables.

Put on your thinking cap and consider how these variables might be related to leaf shape. What hypothesis do you make for how leaf shape might relate to these climatic variables? For this lab, stick with using the continuous explanatory variables. Work with your group to generate a hypothesis. Once you have a hypothesis, come up with at least 3 specific predictions for particular variables.

4 Data Collection with ImageJ

Download the zipped folder “Cercis Images” from the button below. Unzip and open the folder. The name of each image file contains a number referring to the record number assigned by the Butler Herbarium. Later, we’ll use this information to combine our new measurements with the same records in the climate dataset mentioned above.

Open and take a look at some of the images. These are each scanned images of herbarium sheets, exactly as they appear in the herbarium, but with a scale bar and color key added for the scanning process. Take a moment to look at the shape of the apex and sinus of each of your leaves. The apex and sinus shapes have already been scored for you in the dataset, using the ratings in Figure 4. You will be measuring the length and width of 2 leaves for each of the images in the folder.

Open ImageJ: it will appear only as a floating, thin toolbar on your screen. (Link at top of first page if you haven’t already installed it.) Now, click on the toolbar so you are in the ImageJ application. Click File $\rightarrow$ Open… on the menu at the top of the screen. Then find your images and select one to open. Note: if you simply double-click on an image, it will open in Preview, NOT in ImageJ.

Notice the ruler visible in the image, usually in one of the corners. We will use this to set a conversion between pixels and length in mm for our measurements. Fortunately, all of our images were taken from the same distance from the surface and are scanned at the same resolution, so we only set this scale once.

Go to Analyze $\rightarrow$ Set Measurements and make sure that the only checked boxes are “Display label” and “Add to overlay”.

Find the largest leaf in the image for which you can measure the length and width. For slightly damaged leaves, measure the leaf to its undamaged extent. If the largest leaf is partly hidden, try to identify the leaf outline beneath the leaf that’s obscuring it. If this isn’t possible, choose the next-largest leaf.

Go to File $\rightarrow$ Open or type Cmd-Shift-O to open the next image file, and repeat steps 4a-e for the remaining images. (It is ok to close an image file once you have recorded your measurements.) Continue to use L1, W1, L2, W2 for each image.

When you are finished making your measurements, it’s time to save your results file as a CSV file. Click on the Results window, then, on the ImageJ menu bar, navigate to Results $\rightarrow$ Options…. Set “File extension for tables” to “.csv” and click “OK”. To save the actual file, File $\rightarrow$ Save as… (or Ctrl-S/Cmd-S); accept the default file name (“Results.csv”) and save it to your computer’s desktop.

5 Data Management and Preparation

You will use R’s data manipulation capabilities to add your data from ImageJ into the larger WorldClim dataset that you opened earlier.

In RStudio, upload your ImageJ results file, “Results.csv”. Use the read_csv() function to assign the file as an object. We’ll call the new object butler since the specimens are from the Butler University Herbarium:
```
butler <- read_csv("Results.csv")
```
Remember that you measured length and width of two leaves on each of our images. If you view the object butler (View(butler)), you can see that the “Label” column contains the name of the image file with the measurement name added on at the end (after a colon). If you look at just the last 10 rows of the large dataset, bioclim[446:455, ], you can see that the values in the “Accession.No” column match those in your dataset (in the filename of the image). You’ll use that information to add your data to the bioclim dataset.

In looking at the last 10 rows of the bioclim dataset, you may also see that the variables we measured have different names than you used AND they are arranged in separate columns whereas your butler object has all the measurements in a single column. You need to rearrange your butler dataset to match the format of the bioclim dataset.

One more thing to do before you merge your data into the bioclim dataset: there are extra columns in the bioclim data that you need to create based on the measurements that you made:

`bioclim` Variable	Value
Lf.Length.Av	Average leaf length
Lf.Width.Av	Average leaf width
WL.Ratio	Width to length ratio (average width / average length)
Lf.Area.Prox	Leaf area proxy ((2/3)(average lengthaverage width))

Go ahead and create those columns in the butler dataset:

butler <- butler %>%
  mutate(Lf.Length.Av = (Lf.Length1+Lf.Length2)/2, 
         Lf.Width.Av = (Lf.Width1 + Lf.Width2)/2, 
         WL.Ratio = Lf.Width.Av / Lf.Length.Av, 
         Lf.Area.Prox = (2/3)*Lf.Width.Av*Lf.Length.Av)

butler # make sure it worked

(Remember to keep notes for yourself in your R script, using the # to “comment out” the notes so R will ignore them.)

Finally, you’re ready to add your data to the bioclim dataset! We’ll use a handy function called rows patch() to do the replacement. It will look for rows that match Accession.No between the two datasets and then only replace values that are NAs.

6 Considerations of Data Analysis

When we analyze data, we need to consider the type of data that we have collected and the relationship(s) we are testing for to decide what analysis to perform and how to graph our results. First, we need to think about our variables: which are the explanatory variables (i.e., independent variables) and which are the response variables (i.e., dependent variables)? In this case, the variables we measured or calculated about leaf size and shape are our response variables, plus the variables sinus shape and leaf apex, which were provided to us. We might hypothesize, for example, that leaf size and shape relate to the climate a plant experiences. Earlier in this lab, we suggested that a more acute leaf tip (leaf apex) would serve to help water drip off in cool, wet climates. Meanwhile, smaller leaves without an acute apex could minimize surface area to reduce water loss in warm, dry climates. Thus, we have our leaf shape response variables and the the explanatory variables are provided in the bioclim dataset. They include year collected, latitude, longitude, elevation, mean temperature, and mean precipitation.

Now that we’ve clearly identified our variables, consider what type of variables they are: continuous/quantitative (e.g., temperature)? or categorical/discrete (e.g., sex or species)? What type(s) of variables are we using in this lab?The type of data you are plotting and analyzing determine how you graph and analyze the data. In this case, most of our explanatory variables are continuous while a few are categorical (e.g., State). But for today, we’ll just work with the continuous explanatory variables. Meanwhile, our response variables are continuous (or we’ll treat them that way). If we want to know whether leaf area correlates with mean precipitation, what kind of graph would we make?

Before we go any further, let’s visualize what we are trying to do by graph-ing our two variables. When we make graphs, we usually put the response variable on the y-axis (vertical) while the explanatory variable goes on the x-axis (horizontal). Use the axes provided to draw the relationship you ex-pect to observe if our hypothesis is true (about leaf area and precipitation). Be sure to label the axes (including measurement units!).

Another important element of a good figure is the caption. A figure caption describes to the reader the relationship being displayed, which must include the variables involved in that relationship. The caption makes it clear which variable in the figure is the dependent variable and which is the independent variable. What could be a descriptive caption for your figure? Write it below the figure with a numeric label. For example, “Figure 1. Testing for the relationship of precipitation with leaf area. Linear regression yielded a statistically significant relationship (P < 0.0001) with y = 2.2x + 2378.9. Leaf area increased with mean precipitation.” [Note: the p-value is made up, but does it indicate significance?]

To test our predictions, we will perform statistical analyses using simple linear regression to create a predictive model for a response variable as a function of one explanatory variable. In the example of leaf area and precipitation, the model would predict the value of leaf area based on a given value of precipitation. For each combination of a response variable and an explanatory variable we will run 1 linear regression, predicting a linear relationship between those two variables (in reality you can do more complicated models with multiple explanatory and response variables but we’ll stick to the basics for now). A statistically significant analysis (P-value less than 0.05) supports the idea that the response variable differs predictably for values of the explanatory variable. All tests will report P-values as well as a test statistic that is a measure of how much difference is present – in this case the slope of the line and the amount of variance explained.

In future labs we’ll sometimes have categorical variables to analyze and then we’ll have to use a different method, not linear regression. In general, here’s a table with some guidance about what type of graph and what type of analysis is useful for the types of variables we will encounter:

Explanatory Variable	Response Variable	Graph to use	Analysis to use	Values to report
Continuous	Continuous	Scatterplot (`geom_point`)	Linear regression (`lm`)	Slope, y-intercept, P-value
Categorical	Continuous	Boxplot (`geom_boxplot`)	ANOVA and Kruskal-Wallis	P-value for explanatory variable

Below are instructions for one analysis using regression and explaining how to interpret the output. You will use that example to test a couple of your own predictions. But first, before running any analyses, you need to make some graphs and see what patterns might be present in your data.

7 Data Visualization in R

Do you remember what kinds of predictions we might make for this dataset? Write down a few ideas about which variables are likely related to each other and how they are related. For example, in the earlier example with precipitation and leaf area, we predicted that leaves should be smaller in drier climates, so we would expect a positive correlation between precipitation and leaf area.

You should begin by making some graphs of your data, particularly the variables that you plan to analyze but don’t neglect the other variables—you may want to revise your predictions in light of the patterns that you see.

Let’s do an example with the prediction listed earlier, that leaf area will get smaller as precipitation decreases. Let’s see if it looks like that happens in our dataset. To make graphs, we’ll use a function called ggplot() that we used in the pre-lab exercise. The ggplot() function tells R that we’re going to make a plot and then we next specify a function that determines what kind of graph we want to make.

Scatterplot. Since precipitation and leaf area are both continuous variables, then we know we want to make a scatterplot, which uses the geom_point() function:
```
bioclim %>%
  ggplot() +
  geom_point(mapping = aes(x = Mean.Precip, y = Lf.Area.Prox)) + 
  xlab("Mean Precipitation") +
  ylab("Leaf Area")
```
There is a lot of scatter but it does look like leaf area is increasing with precipitation. But remember the prediction had to do with precipitation AND temperature where warm/dry corresponded to smaller leaves so a negative correlation between temperature and leaf area. Let’s check out the relationship with Mean.Temp. Change the code above to graph temperature instead of precipitation. That also follows our prediction! I wonder what the relationship is between temperature and precipitation…

Go ahead and make graphs for some of the variables involved in your predictions. And make any additional graphs that you are interested in exploring.

8 Data Analysis in R

After you have graphed the data, you will run the appropriate statistical tests to test your predictions. This means you will have a statistical model (relationship between explanatory and response variables) for each test that you run. Before you run your own analyses, we’ll walk through an example of linear regression so you will know how to do it.

Feel free to talk over ideas with your classmates and instructors but you should perform the analyses on your own. Do not hesitate to ask your instructors for help with your graphs and analyses—you are not expected to have mastered these skills, you’ve only just begun to learn them!)

8A Linear Regression

Linear regression is appropriate when both your response and explanatory variable are continuous. Linear regression essentially estimates a line of best fit for our data. We are assuming that our variables will change in a straight-line way, this method does not account for any curvature in the relationship, only straight lines! The straight line relationship estimated by the regression model tells us how much change in the explanatory variable (x-axis) relates to how much change in the response variable (y-axis). Thus, when we do a linear regression, the information we report to describe the output is the slope and y-intercept of the estimated regression line. We then also have a P-value that corresponds to how likely it is that the slope of the line is zero. A small P-value (less than 0.05) means the slope is probably not zero, which we interpret as statistical significance, there is evidence of a relationship between our two variables.

Below, we’ll work through an example with leaf area as our response variable and precipitation as our explanatory variable, as we used for the graph above. But first, let’s talk about what is included in the output of a linear regression. Simple linear regression analysis allows us to quantify the relationship between leaf area and precipitation using the following:

Regression equation: This is an equation for the line describing leaf area ($y$) as a function of mean precipitation ($x$), of the form $y = b + mx$ (where $b$ is the y-intercept and $m$ is the slope of the line).
P-value: As in the chi-square analysis we used in an earlier lab exercise, a probability of 5% or lower will be considered statistically significant. Here, our null hypothesis will be ‘there is no association between leaf area and mean precipitation.’ Thus, the P-value gives us the probability that the slope of the line is not different from zero (which would imply zero relationship between the variables).
R² value: The R-squared value measures how much of the variation in leaf area is explained by variation in mean precipitation. This value ranges between zero (no variation explained) and one (100% of the variation is explained).

Now let’s do the example analysis. And after we run the regression, we’ll add the data from the analysis to the graph we made earlier.

It’s really easy to run the linear regression and we’ll go ahead and save the results in case we wanted to look at them again later. Remember to choose descriptive names when you create new objects! In this case, we’ll save the output to an object called leafarea.precip.mod. Then we’ll ask R to print the object to the screen so we can see the summary.
```
leafarea.precip.mod <- summary(lm(Lf.Area.Prox ~ Mean.Precip, data = bioclim))

leafarea.precip.mod  # Print the results of the regression model
```

From the results summary, you can see the P-values for the intercept and slope (the Estimate for ‘moisture’) and the R-squared value. Your results should look similar to the image below and we should notice a few things:
- The Estimate column contains the value of the y-intercept, (Intercept) = 2378.8818 leaf area units at zero mean precipitation units.
- The slope is the Estimate value for Mean.Precip: +2.2033 leaf area units for every unit increase of mean precipitation.
- For the R-squared (R²) value, we use the Adjusted R-squared = 0.0537 or approx. 5.3%.
- The P-value for our slope is listed both in the Coefficients table under Pr(>|t|) AND on the last line of the output, after the F-statistic. P = 0.0000004107. We can abbreviate that as P < 0.0001.

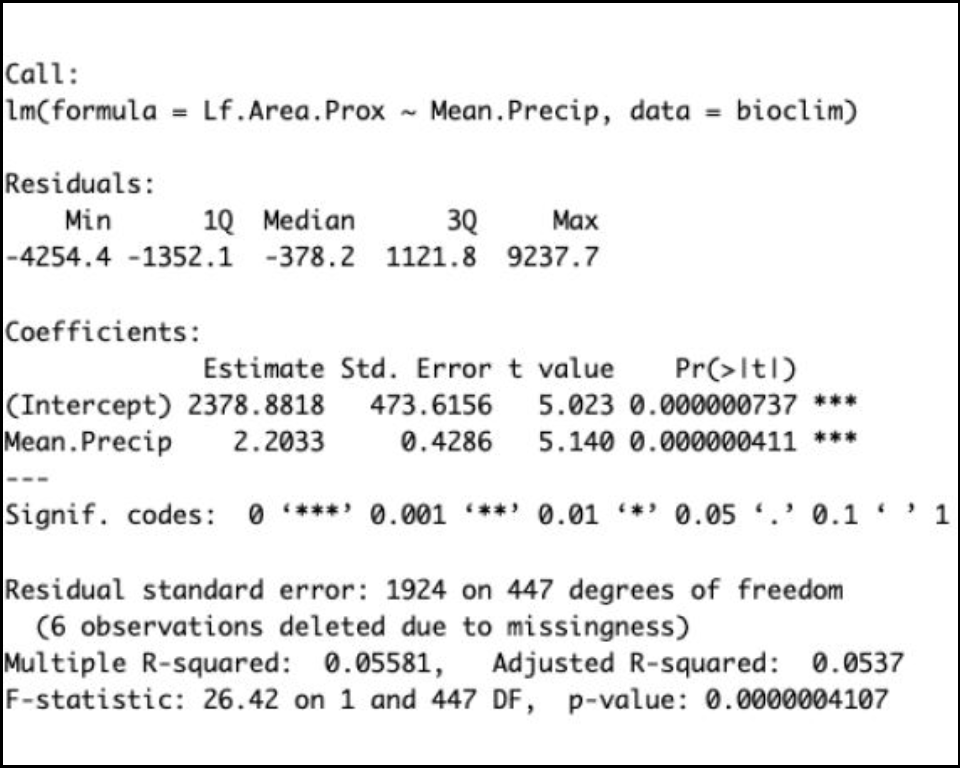
With that information, we can write the regression equation! For the above output that looks like (using 2 significant digits and rounding): $y = 2378.88 + 2.20x$. Is the slope significantly different from zero in this example?

The final thing we want to do is be sure to add the slope, P-value, and R² value to our graph.

bioclim %>%
  ggplot(mapping=aes(x = Mean.Precip, y = Lf.Area.Prox)) +
  geom_point() +
  xlab("Mean Precipitation") +   # Add a x-axis label
  ylab("Leaf Area") +  # Add a y-axis label
  ggtitle("Leaf Area as a Function of Mean Precipitation") +  # Add a plot title
  geom_abline(slope = 2.2, intercept = 2378.88) +  # Add the regression line
  # Add the equation, R^2, and P-value of the regression with annotate function
  annotate("text", label = "Y = 2378.88 + 2.20X", x = 1450, y = 12500, size = 3.5) + 
  annotate("text", label = "R-sq = 0.05, P < 0.0001", x = 1450, y = 12000, size = 3.5)

9 Post-Lab Assignment Due Next Lab Period

Each group of 2 should test 2 additional predictions beyond the leaf area versus precipitation example carried out in these instructions. Combine informative, nicely formatted graphs and tables into a document with the relevant P-values next to the graphs. Include typed answers to the following questions and turn them in with your figures. Support your answers by referring specifically to your figures and/or the results of your tests of significance, where appropriate.

Submit responses to the Lab File Submission form for your lab section (the link can be found along the top menu bar of this page).

Write out the hypothesis and then each of the predictions that you chose to test in this dataset. Be sure to specify the relationship that you predicted between your explanatory and response variables for each prediction.

Which statistical analyses did you choose to perform to test your predictions, and why? Explain how these comparisons could help test your hypothesis.

Explain the results of your analyses in paragraph form, indicate if they support your hypothesis, and explain how strongly they may support your hypothesis. For each result, provide at least a P-value, the type of analysis performed, and a relevant figure with appropriate labels. Support your explanation with information from your figure and analyses.

Adaptive morphology can result from development in response to the environment over the lifetime of an organism—called phenotypic plasticity—or from selection across generations. Discuss how either or both of these mechanisms might work or interact to alter the morphology of Cercis. (There is no right answer—just think about the different ways that adaptation can occur.)

Lab 7. Adaptive Morphology of N. American Redbud Trees (Cercis canadensis)

April 02 & 03, 2024